上上篇 基础知识
上一篇 习题总结1
记号:
-
在提及两端点情况下,用 表示一条容量为 ,费用为 的边,下同。
-
用 来表示从 向 连一条容量为 ,费用为 的边,下同, 有时会省略。
类型4:最小割
最小割主要解决的是这样的问题:求满足某种条件(要转化为源点和汇点不联通)的最小代价。
一个小模型
这里有个能在部分题中用上的模型:
有若干个东西,每个东西都有一些价值。
还有若干个限制,对于每个限制,有若干个物品不能同时选(即必须有至少一个不选,通常为两到三个)。
那么把每个物品拆点,连边容量为价值。
然后对于每个限制,用边从源点到汇点串起来(边权 ,可能要安排顺序,形成环的话很麻烦),求最小割,答案就是总价值减去最小割。
解释:每个限制体现在图中都是一些路径,而这中的每条路径都要割断一些点,让源点和汇点不联通,用网络流完成最优的决策,即删除的点代价最小。
P2774 方格取数问题
https://www.luogu.com.cn/problem/P2774
给定一个网格图,从网格中选取若干个数,使选取的格子没有公共边,求取出的数最大的和。
相邻的两个格子不能同时取,显然就是上面的模型了,黑白染色一下,然后源点连黑的,容量为格子中的数字,然后黑点连相邻的白的,容量 ,白的连汇点,容量为格子中的数字。
P3355 骑士共存问题
https://www.luogu.com.cn/problem/P3355
在一张 的方格国际象棋棋盘上,马可以攻击的范围如下图所示:
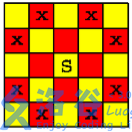
有些格子设置了障碍,不能进入,求最多放置多少匹马,使它们互相不攻击。
黑白染色后,一匹马能攻击到的格子的颜色恰好是和它在的格子颜色相反,并且假如 能攻击到 , 也能攻击到 。
假如一条点有障碍,在加边的时候忽略它即可。
和上一题差不多。
源点连黑点,黑点连能够攻击到的白点,白点连汇点。
P2762 太空飞行计划问题
https://www.luogu.com.cn/problem/P2762
有 个实验,每个实验 收益 ,有 个仪器,买仪器 花费 ,每个实验 需要某些仪器 ,仪器可以重复使用,问最大收益,并输出方案。
这题是最大权闭合子图问题,关于这个问题,不过多介绍,考虑用上面提及的模型解决。
发现这题的限制是:选实验 和不选仪器 。
发现「不选」的条件有点特殊,考虑怎么处理。
在模型中,先选上所有的物品,然后减去最小的代价,一个物品的代价就是选它减不选它对答案贡献的差。
实验 ,不选它贡献为 ,选它贡献为 。
不选仪器 ,不选它贡献为 ,选它贡献为 。
答案为
按照上面模型的方法建图,不过由于只有两个限制,不用拆点。
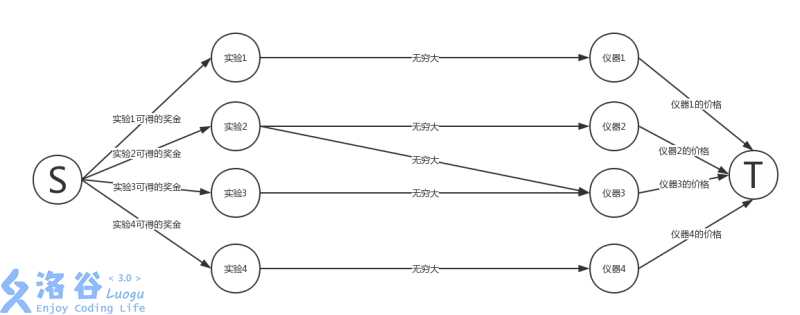
从源点向实验节点 连 的边 ,从仪器节点 向汇点连 的边,从实验节点 向所有 连 的边,跑最小割,然后用 减去最小割就是答案。
还要输出方案数:做实验 ,说明源点到 的边没被割,买仪器 ,说明点 到汇点的边被割了。
P4174 最大获利
https://www.luogu.com.cn/problem/P4174
有 个基站,每个基站需要 的成本,有 个用户,需要基站 和 ,可以获利 。
求最大获利。
和上一题差不多,源点连用户,容量 ,用户 连基站 和 ,边权 ,基站 连汇点,容量 。答案为 。
P5458 水晶
https://www.luogu.com.cn/problem/P5458
地图由若干个密铺的六边形单元组成,如下图所示,为了方便,用 表示一个格子,表示从原点开始,按所示的 轴走了 步,注意一个格子可以由多个坐标表示。

有 块水晶在地图内,第 块的坐标为 ,每块有 的价值,注意一格内可能有多块水晶。
满足 的格子内有能量源,有能量源的格子内的水晶的价值多 。

会形成两种共振:
-
共振,如果三块水晶所在的格子排列成一个三角形,会有 共振。

-
共振,如果三块格子所在单元连成一条直线,并且中间的格子有能量源,会有 共振。

你要破坏一些水晶,使不会有共振,并且留下的水晶价值最大。
由于在平面上,只需要两个坐标就够了,要把格子的坐标转换。
发现往 轴走 格,可以转化为往 轴走 格,往 轴走一格。

所以 被转化为 ,并且
故新旧坐标加起来模 不变。
而题目中 的格子有能量源也提醒了我们可以按 对格子分类。
考虑什么样的有水晶的格子会形成共振。


不难发现,假如一个模 余 的有水晶的格子旁边有一个余 和余 的有水晶的格子,那么会引发共振。
根据上面的模型,我们可以这么建图:
拆点,每个有水晶的格子拆成入点和出点,之间连边容量为水晶的价值。
源点向所有模 余 的点连边,余 向相邻的余 的点连边,余 向相邻的余 的点连边,余 向汇点连边,这些边边权均为 。
然后价值和减去最小割就可以了。
另一个小模型
这个模型可以用在一些需要二选一的问题上。
需要作出 个一些二选一的抉择,设为 和 ,每个选 或者选 都能有一定价值,同时若干个同选 或者同选 也能有一定价值,问最大价值。
形式化来说:
有 个数,记为 , 可以为 或 。
同时有若干个条件,记为 ,假如对于 都有 ,那么可以有 的价值。
问最大价值。
我们考虑用联通性来表示一个选择。
如 与 联通,那么选 ,否则要与 联通,选 。
我们考虑加上所有的价值,然后删去尽可能小的,满足「二选一」,可以试着用最小割。
对于每个条件,新建一个节点 ,若 ,从源点向 连 的边,然后对于 ,从 向 连 的边;若 ,反过来即可,即 。
答案就是价值和减最小割。
为什么是正确的呢?
考虑一个点选 ,那么就要割断所有与 的路径。
这样所有要这个点选 的条件都不会对答案有贡献了。
P4313 文理分科
https://www.luogu.com.cn/problem/P4313
有一个班级,要文理分科,这个班级可以用 的矩阵表示。
对于 :
- 选文科,可以获得 的满意值,假如和他相邻的人都选了文科,额外获得 的满意值。
- 选理科,可以获得 的满意值,假如和他相邻的人都选了理科,额外获得 的满意值。
问所有人最大满意值之和。
显然就是上面的模型:
对于自己:
, ;
对于周围的人,令 是两个为处理 和 的节点,设 为和 相邻的点。
, , 。
, , 。
P1646 happiness
https://www.luogu.com.cn/problem/P1646
有一个班级,要文理分科,每个人选文科,选理科,相邻的两个人选文科或理科会获得喜悦值,求最大喜悦值之和。
和上面那题几乎一模一样。
源点向每个人连容量为选文科可以获得的喜悦值的边。
对于每对相邻的人,新建一个点,源点向那个点连容量为那对人同时选文科可以获得的喜悦值,然后那个点向那两个人连边。
理科同理,不过反过来。
CF311E Biologist
https://www.luogu.com.cn/problem/CF311E
有一个长度为 的 串 ,将第 个位置变为另一个数字的代价为 。
然后有 个要求,每个要求给定 个位置(设为 ),要求这些位置同为 ,假如满足,有 的利润,否则,部分要求要倒给 。
求最大收益。
这一题比较不同的地方就是要部分条件要倒给 或者 ,考虑使用 P2762 的方式解决,使得割边时能够把它们剪掉,留着时不计入答案。
建边方式:
若 , ;否则 , 。
对于每一个限制 ,新建点 ,若 , ,若 , 。
答案为 。
类型5
这种类型要解决的问题大多可以转化为这样的一个模型:
有一个有向图,求一个子图,满足点 的入度不大于 ,出度不大于 ,边数尽可能多,求最小费用或最大收益。
建图方法如下:
对于每个点 ,拆成两个点 和 ,然后 。如果原图中有一条边 ,那么连边 。
然后跑最小费用最大流。
为什么?
考虑一条边 如果被选了,即在网络流中 流量为 ,那么 的流量会多 , 的流量会多 。因为 的流量限制为 ,故这里只能连 条边,满足出度小于等于 的限制,入度限制同理。
最大流可以保证选至多的边,在很多情况下保证跑满入度或出度,而最小费用保证费用最小。
CF277E Binary Tree on Plane
https://www.luogu.com.cn/problem/CF277E
给定平面上的若干个点,要求组成一棵二叉树,若 是 的父亲,必须要有 ,两个点相连的边权定义为两个点之间的欧几里得距离。
求最小二叉树边权和,或报告这样的二叉树不存在。
是上面提及的这个模型,每个点入度小于等于 ,出度小于等于 ,每个点向所有 比自己小的点连边。
连边方式:
,
跑最小费用最大流,假如最大流小于 则无解。
P2764 最小路径覆盖问题
https://www.luogu.com.cn/problem/P2764
给定有向图 ,设 是 的一个简单路(顶点不相交,特别的,路径长度即所含路径条数可以为 )的集合,如果 中的每个顶点恰好出现在 中的一条路上一次,那么称 是 的路径覆盖,求最小路径覆盖,即 最小的 。
每个点在一条路径上,说明入度小于等于 ,出度小于等于 。
按照上面的模型建边,得到最多有 条边,那么最少要 条路径,因为 个点的入度为 ,剩下都为 ,而每个入度为 的点都是一条路径的开头。
输出方案也很简单,如果 跑满了,说明选 ,得到原图的一个子图,就容易输出了。
P2765 魔术球问题
https://www.luogu.com.cn/problem/P2765
有 个柱子,依次向柱子上面放 的球,要求同一个柱子两个相连的球加起来是一个完全平方数。
把球看成点,把能放在一起的球连起来,需要多少个柱子,就是这个图的最小路径覆盖。
从 开始,不断向图中加点,假如加到 ,找出图中所有 能放在上面的点 ,即 , 向 连边,直到这个图的最小路径覆盖大于 。
P1251 餐巾计划问题
https://www.luogu.com.cn/problem/P1251
一个餐厅在 天中,第 天需要 块餐巾,每天,餐厅可以购买餐巾,每块 分,在第 天晚上,餐厅可以把旧餐巾送到快洗部,每块 分,能在第 天早上收到餐巾,也可以送到慢洗部,每块 分,在第 天早上收到餐巾。
和我们的模型大抵相符,不过有需要改动的地方,介绍一种采用这种模型思想建图的另一种解释。
把每一天拆成早上和晚上,分别为 和 。
表示每天晚上收到 块脏餐巾。
表示每天早上需要 块干净餐巾。
每天早上可以购买餐巾。
晚上不洗可以留到第二天。
送到快洗部。
送到慢洗部。
跑最小费用最大流即可。
P4553 80人环游世界
个国家,按从东向西的顺序给出,某些国家之间有航线, 个人旅游,每个人可从任意国家开始,在任意国家结束,从东向西游历若干个国家,注意路线上相邻的两个国家必须由航线直接相连。
同时第 个国家有且仅有 个人游历。
问最少机票钱。
考虑先建出模型中的原图,在根据模型建出跑网络流的图。
可以从任意地方出发,所以设一个出发点 ,出度 ,结束点 ,入度 ,然后每个国家 ,出度 ,入度 。
可以从任意地方开始或结束。
若 和 之间有航线,机票一人 ,且 : 自东向西,要航线相连。
根据模型,建出跑网络流的图,然后跑最小费用最大流即可。